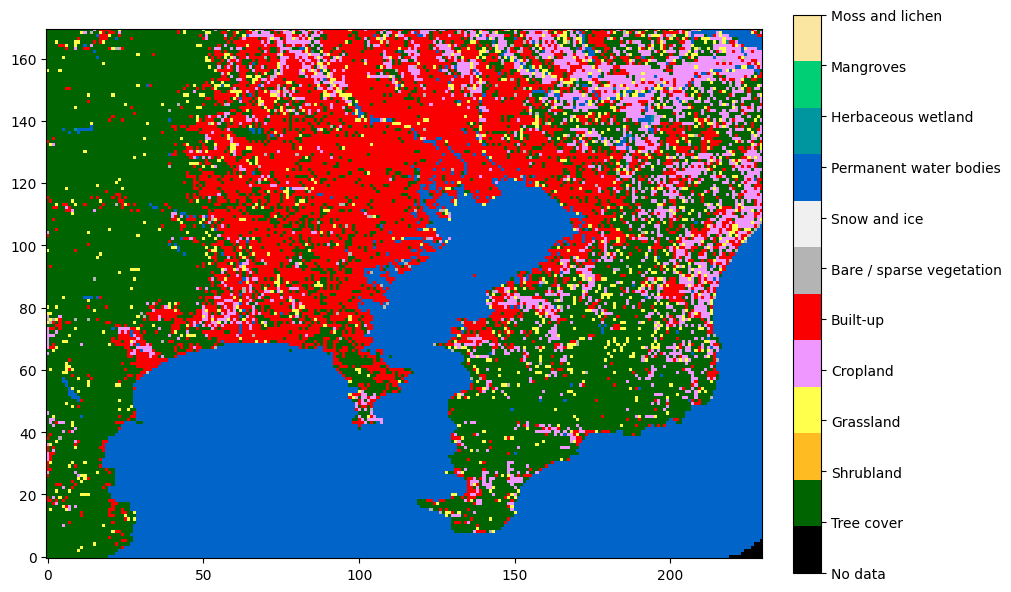
Extracting regions from ESA WorldCover

ESA WorldCover is a categorical dataset with 11 classes of land cover (such as water, trees, built-up etc.) at a 10-meter resolution covering most of the world. In this short post I show how to extract a specific region given its geographic coordinates.

Acquiring the data

The dataset is delivered in tiles covering 3x3 degrees each, bundled into macrotiles of 60x60 degrees. The macrotiles can be freely downloaded on the project’s website.

Assuming you have downloaded and extracted the correct macrotile, you can use the rasterio package to load the tile corresponding to the given geographic coordinates:

import rasterio

def load(lat_lon):
    # dataset is provided in the form of tiles 3x3 degrees in size
    # compute tile coordinates
    tile_coords = (int((lat_lon[0] // 3) * 3), int((lat_lon[1] // 3) * 3))
    tile_extent = (tile_coords, (tile_coords[0] + 3, tile_coords[1] + 3))

    # build file name
    lat_str = (f"N{abs(tile_coords[0]):02d}" if tile_coords[0] >= 0 else
               f"S{abs(tile_coords[0]):02d}")
    lon_str = (f"E{tile_coords[1]:03d}" if tile_coords[1] < 180 else
               f"W{(360 - tile_coords[1]) % 360:03d}")

    filename = f"ESA_WorldCover_10m_2021_V200_{lat_str}{lon_str}_Map.tif"

    with rasterio.open(filename) as dataset:
        data = dataset.read(1)  # read first band

    return data, tile_extent

Extracting the region of interest

Now, suppose we have a region of interest specified as a tuple of min-latitude, max-latitude, min-longitude, max-longitude. We now need to “cut out” this area out of the full tile.

The key to this is a function called discretize_extent. It takes 3 parameters:

• extent of the tile we have loaded
• shape of the tile (X & Y resolution)
• the requested region

…and returns the raster (integer) coordinates corresponding to the region within the tile. Note that by snapping to the integer coordinates, the geographic coordinates will slightly change as well and must be recomputed. Given the high resolution of the dataset, this inaccuracy will be usually negligible, but we like to do things properly, so I also recompute the updated extent.

We follow the convention given by ISO 6709:

1. Latitude comes before longitude
2. North latitude is positive
3. East longitude is positive
4. Coordinates are represented as decimal degrees

On the other hand, rows in the dataset are ordered north-to-south, which means that at some point, we need to flip the Y coordinate.

import math

def discretize_extent(tile_extent: tuple[tuple[float, float], tuple[float, float]],
                      tile_shape: tuple[int, int],
                      requested_extent: tuple[tuple[float, float], tuple[float, float]]):
    # axis 0 is latitude north->south (!)
    # axis 1 is longitude west->east

    (tile_min_lat, tile_min_lon), (tile_max_lat, tile_max_lon) = tile_extent
    (req_min_lat, req_min_lon), (req_max_lat, req_max_lon) = requested_extent
    relative_extent = ((req_min_lat - tile_min_lat,
                        req_min_lon - tile_min_lon),
                       (req_max_lat - tile_min_lat,
                        req_max_lon - tile_min_lon))

    print(f"{relative_extent=}")

    # project user extents into raster space
    px_per_deg_lat = tile_shape[0] / (tile_max_lat - tile_min_lat)
    px_per_deg_lon = tile_shape[1] / (tile_max_lon - tile_min_lon)

    print(f"{px_per_deg_lat=} {px_per_deg_lon=}")

    # snap "outwards" to integer coordinates
    min_y = int(math.floor(relative_extent[0][0] * px_per_deg_lat))
    min_x = int(math.floor(relative_extent[0][1] * px_per_deg_lon))
    max_y = int(math.ceil(relative_extent[1][0] * px_per_deg_lat))
    max_x = int(math.ceil(relative_extent[1][1] * px_per_deg_lon))

    # sanity check :)
    print(f"{min_y=} {min_x=} {max_y=} {max_x=}")
    assert min_y >= 0 and min_y <= tile_shape[0]
    assert min_x >= 0 and min_x <= tile_shape[1]
    assert max_y >= 0 and max_y <= tile_shape[0]
    assert max_x >= 0 and max_x <= tile_shape[1]

    # reconstruct geo coordinates
    discretized_extent = ((tile_min_lat + min_y / px_per_deg_lat,
                           tile_min_lon + min_x / px_per_deg_lon),
                          (tile_min_lat + max_y / px_per_deg_lat,
                           tile_min_lon + max_x / px_per_deg_lon))
    print(f"{discretized_extent=}")

    # flip Y
    min_y_corr = tile_shape[0] - max_y
    max_y_corr = tile_shape[0] - min_y
    print(f"{min_y_corr=} {max_y_corr=}")
    assert min_y_corr >= 0 and min_y_corr <= tile_shape[0]
    assert max_y_corr >= 0 and max_y_corr <= tile_shape[0]

    return ((min_y_corr, max_y_corr), (min_x, max_x)), discretized_extent

In practice you might also want to down-sample the extract for performance or other reasons. Since the data is categorical, there is no point in trying to interpolate the sample values; nearest-neighbor sampling must be used: